ユーザーアンケートなんかを集計すると
「あれ？これってちゃんと有意差あるんだっけ？」となることがあると思う。

統計の検定はそれこそいろんな種類があって、またそれぞれに仮定・条件があるので、
ここでは”とりあえず”という超オーソドックスなものを実際のシーンに合わせて紹介する。

といってもノンパラメトリックやn数などでの場合分けはしない。
とりあえずこれ使っとけば、という感じなのでちゃんと勉強したい人はしてください。

また、そもそものこの記事のモチベーションを解説しておくと、
数字自体はいわゆる”ファクト”として提案や説得の武器になることが多いが、
なんでもかんでも平均をとる、なんでもかんでも差があればいい。みたいな人が多いが、
そこに「待った！」を入れるという発想がそもそもない人が多いと思うので、
理論や厳密な使い方云々の前に、とりあえず検定というものがある。ということを知ってほしい。

原理的なものや哲学的な話はまた別の記事でアウトプットしたい。

営業が覚えておくべき検定まとめ

まず結論だがパターンごとに４つ覚えとくといいと思う。

・平均か、比率か
・データ元（アンケートに答えている人）は同じか、別か

1.　対応のある
2.　対応のない
3.　従属関係
4.　一部従属関係

数式は以下のとおり。
1.$$ T=\frac{(|b-c|-1)^2}{b+c} $$
2.$$ T=\frac{p1-p2}{\sqrt{p(1-p)(\frac{1}{n1}+\frac{1}{n2})}} $$
3.$$ T=\sqrt{n}(p1-p2) $$
4.$$ T=\frac{p-p1}{\sqrt{\frac{p(1-p)}{n}}} $$

例えば趣味についてアンケートを、n=1００・複数回答可・男女にとったとする。

データはこのような感じ

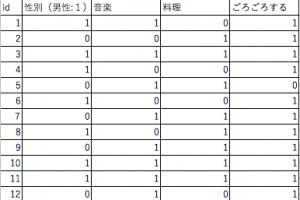
これをとりあえずグラフと図式化してみるとこんな感じ。

ここから一つづつ使い方を見ていく。

１、対応のある：回答どうしの差をみる

”対応のある”とはややこしい書き方だけど、アンケート相手が同一人物であるということ。
例えば薬を飲む前と後での比較とか。
ここでは料理は音楽より人気といえるか？を検定してみる。

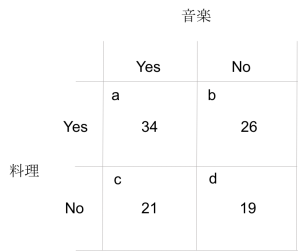
このようなマップでわかりやすくし、計算するとT＝0.34。（マスの左上からabcd）
つまり差があるとは言えない。音楽と料理どっちが人気かぶっちゃけ分からんという結論になる。
これはどっちかだけ！(bとc)という硬派がどれだけの差でいんの？って話で、
よく広告でアンケート調査を見かけるが5％程度の差ならサンプル数500はホシイ。
また5％と10％での差など低い値同士だともっと数が必要になる可能性もあるので気をつけたい。

2.対応のない：男女別の差をみる

対応のないとは１．と違いそもそも違う属性のもの。
ここでは男女で差があるかを見ている。

男女で切って結果をみていると以下のようになった。

女性の方が趣味に意欲的に見えるがまあそれは置いておいて、
なにやら女性の方がごろごろするのが好きらしい。
このごろごろすることの男女の差はあるのだろうか？
上の式を使って計算シてみる。(pは全体の割合なので70/100=70%)
計算の結果T=1.82　これも差があるとは言えなさそうだ。
とすると他の項目も差があるとは言えないだろう。
つまりぶっちゃけ男女の違いはこのアンケートでは分からんということになる。

3.従属関係：50％付近のYes/Noの差をみる

これはどちらか一方が増えればどちらかが減るというゼロサムゲーム的な感じのもの。
例えば世論調査で微妙なラインで55％とか来たときに使える。
ここでは音楽が趣味な人は過半数以上いるのか？ということを見てみる。
上の式からT=1ということでぶっちゃけ過半数以上とはいえない。という結論となる。
料理はギリギリ言えそうだ。(p1はYes,p2はNoの比率)

4.一部従属関係：女性と全体の差をみる

これは年齢別に10世代に区切ったとして、90代だけ以上に特徴的！というようなときに
全体と比較してみたりするときに使う。
ここでは女性がごろごろするのが全体と比べて好きか？をみてみる。
上の式からT=-2.18ということで差がありそうだ。(p1が女性比率)
2.の男女の差では有意ではなかったがなかなかよくわからない結果になった。
全体の中に比較対象を入れるか入れないかの差だと思うが、詳しい人教えてください。

今回は実務で使う、もしくは気をつけるものをまとめたが、
基本的に上記はどれもYes/Noの二値変数を正規分布に近似しているので、
どのnも30以上であるかは毎度注意した方がよい。