前提
セールスが意識すると良いと思っているデータに対する考え方をWantedlyで以前書いた。
とは言え、どんなデータを貯めるか決めても解析方法が分からないと気分が乗らないと思うので、いくつかの手法とサンプルコードを記載する。
Rは非エンジニアでも扱いやすい言語なので、僕のようなセールスの人間にはかなりオススメ。逆にエクセルなどで解析オプションから統計解析をやる方が、成約が多すぎるので個人的には難しいと思うし、pythonだとデータの型やダミー変数の設定が最初はめんどくさいのでちゃちゃっと単発で結果が見たい時はR一択だと考えている。
サンプルコードとグラフイメージ
手法の解説やコード内のライブラリの解説はしないので、気になるものがあれば検索して下さい。データの記録は質的変数(あり/なし、担当者属性A,B,C)で記録することが多いと思うので、その内容をピックアップしています。
|
1 2 3 4 5 6 |
<s><code>#</code></s><code>データ読み込み d <- read.csv("CSVファイルのパス",fileEncoding='cp932') #概要確認 summary(d)</code><s><code> </code></s> |
|
1 2 3 4 5 6 7 8 9 |
#判別分析 source("http://aoki2.si.gunma-u.ac.jp/R/src/qt2.R", encoding="euc-jp") dat <- d[, 2:7] group <- d[, 1] group <- as.factor(group) result <- qt2(dat, group) summary(result) print(result) plot(result, which="category.score", i=1) |
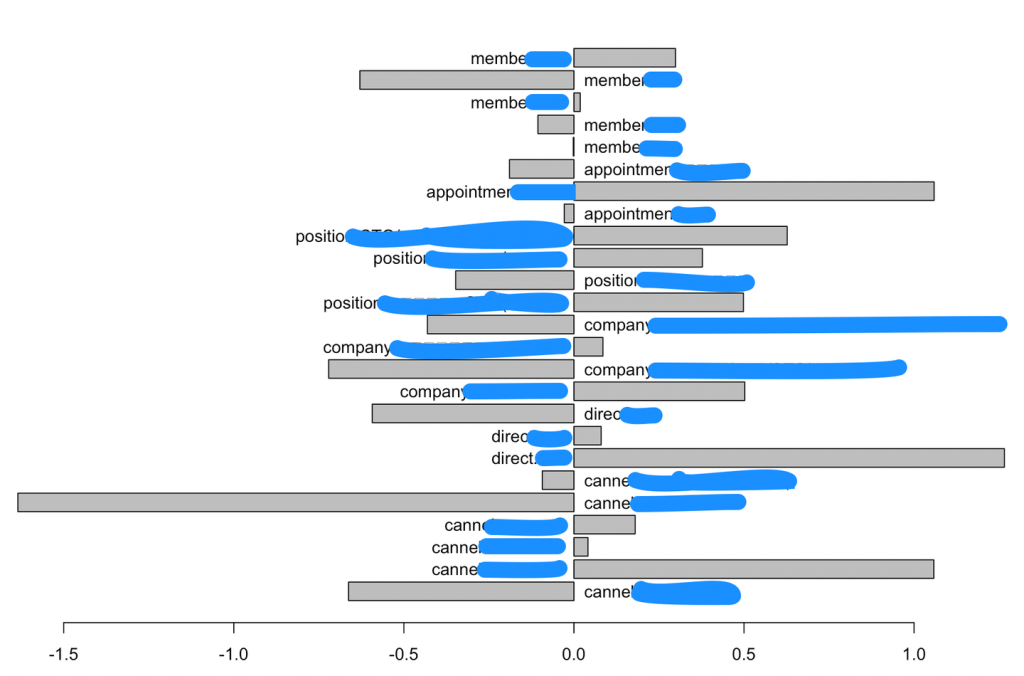
|
1 2 3 4 5 6 7 |
#ロジスティック library(MASS) fit_glm <- glm(y ~. , data = d, family = binomial) step_glm <- stepAIC(fit_glm, dhirection="both") function_summary <- summary(step_glm) #par(mfrow = c(1,1),mar=c(2.5, 10, 2.5, 1)) barplot(exp(fit_glm$coefficients),cex.names=1,horiz=T ,las=2) |
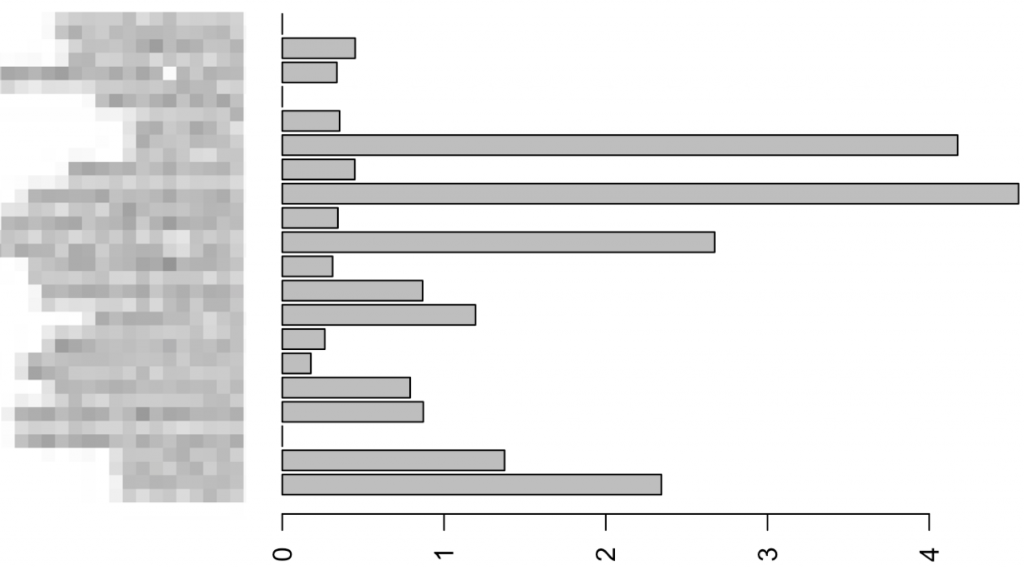
|
1 2 3 4 5 6 7 8 |
#ナイーブべイズ install.packages("e1071", dependencies = TRUE) library(e1071) d$y <- as.factor(d$y) nb.model <- NaiveBayes(y ~., data = d) par(mfcol=c(2,3)) plot(nb.model) summary(nb.model) |

|
1 2 3 4 5 6 7 8 9 |
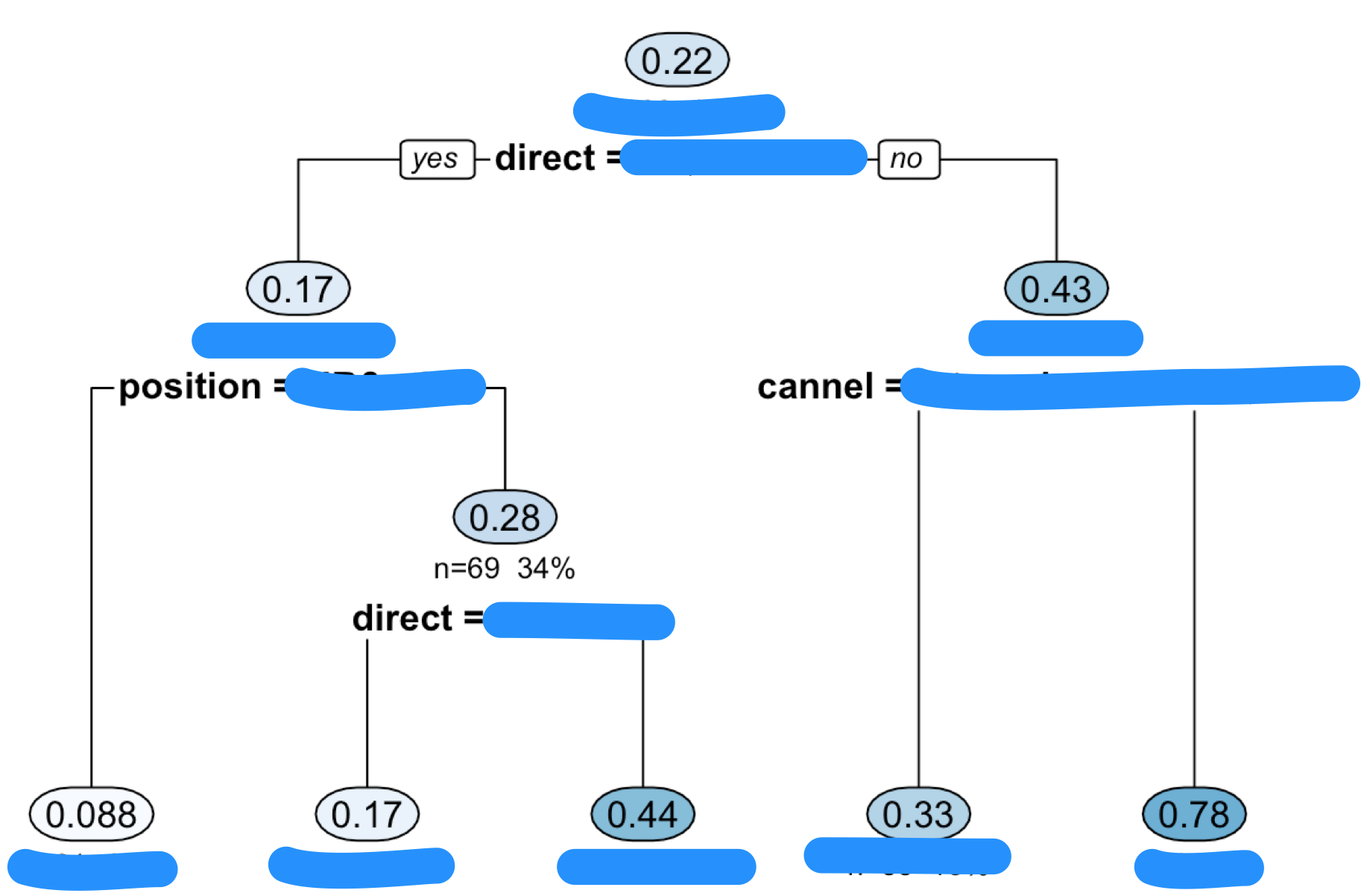
#決定木 library(rpart) library(rpart.plot) library(partykit) ct <- rpart(d$y~ . , data = d, method = "anova",cp=0.027) rpart.plot(ct, type = 2, uniform = TRUE, extra = 101, under = 1, faclen = 0) plot(as.party(ct), gp = gpar(fontsize = 7,fontfamily = "Osaka")) printcp(ct) plotcp(ct) |
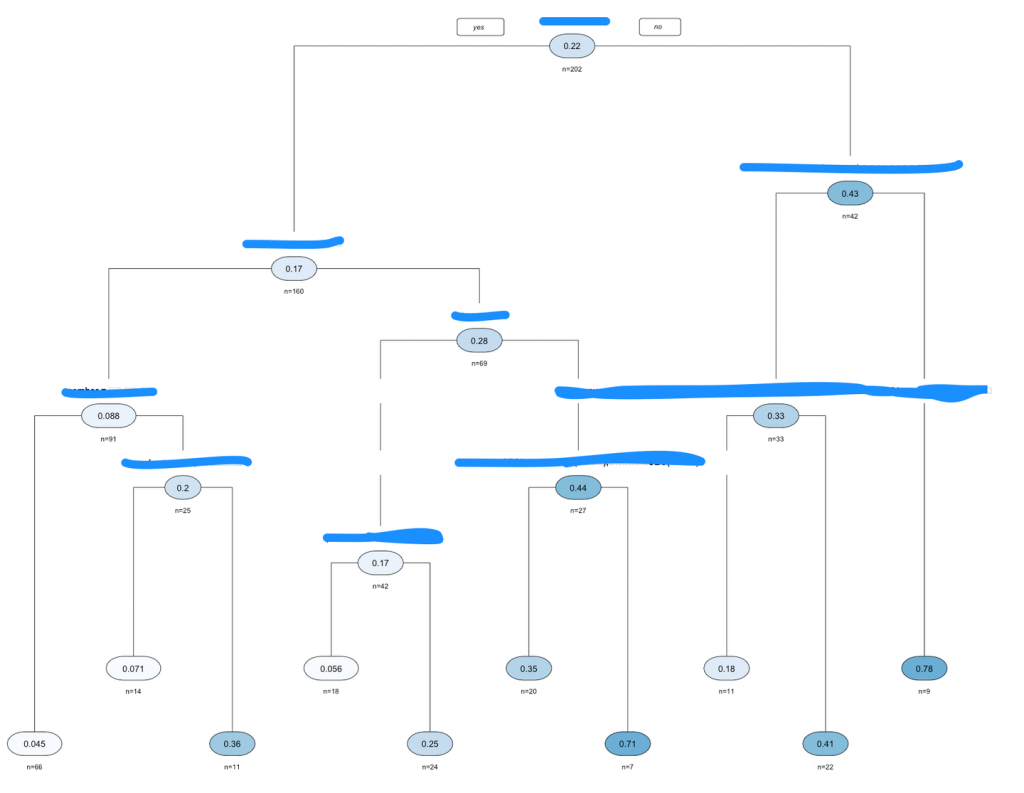
|
1 2 3 4 5 6 7 |
#ランダムフォレスト library(randomForest) tuneRF(d[,1:7],d$y,doBest=T) model = randomForest(y ~ ., data = d,ntree = 7) importance(model) varImpPlot(model) prediction = predict(model, d_pre) |
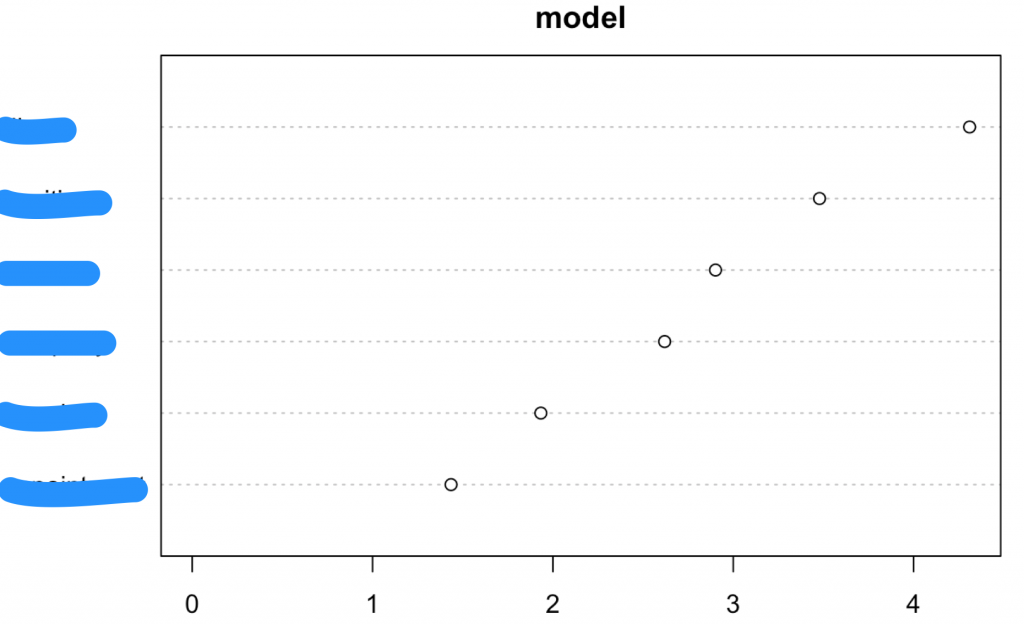
手法の向き不向き、単純集計とどっちがよい?
詳しくはここでは記載しないが、セールスのような少量データだとランダムフォレストはあまり適さない手法だし、判別分析やロジスティックの出力数値もあくまで”手法上の数値”。また説明変数の多さによってほとんど有意差が出ないということも多いので、どれか一つの手法を信じるのではなく(とりあえずぶっこんで出てきたものを鵜呑みにするのではなく)、解析手法の特性を理解した上でそれぞれ参考値として強弱関係を見ることが良い。
だからといって単純集計が良いのかというと、単純集計では多変量の影響を考慮できない事が考えもの。完全にランダム比較ができているのであればよいが実務ではそうも行かないので、それぞれ使い分けが大事という結論です。
|
1 |

コメントを残す