2つの変数同士の相性というか関係性を確認するのが相関係数。
そして説明変数から目的変数の説明力なり当てはまりを表すのが決定係数だが(超ざっくり)、ココらへんは個人的に「ややこしいか〜」と思ったところなので、検索マップとして用語をまとめておく。
そもそもこんなミス、課題感ありませんか?
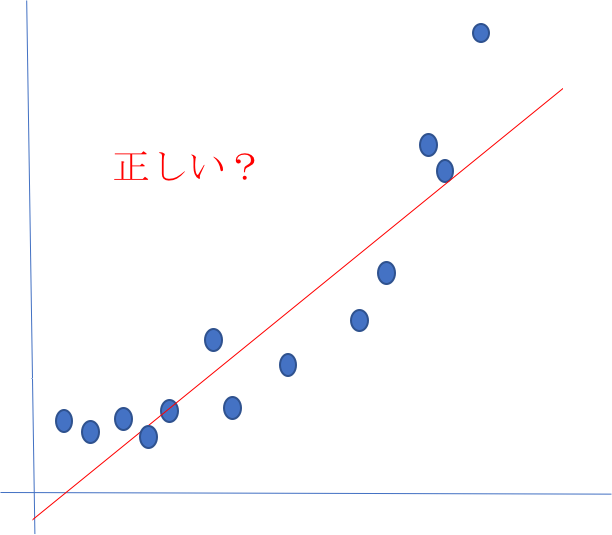
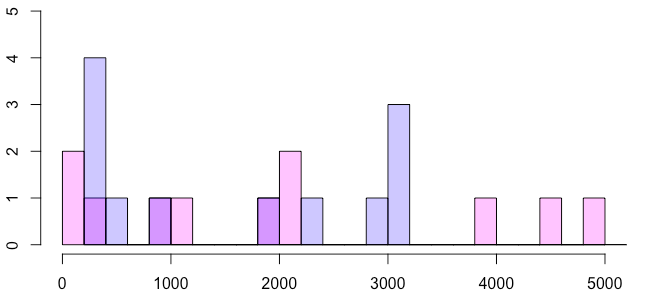
まず相関係数あるあるとして、 ”満足度と売上の相関は?” みたいな問題に、エクセルで相関係数ドン!みたいなことをしている例で、ひどい場合は ”男女(男ダミー)と売上の相関は?” みたいなことも(本当に時々)見る。ここらへんはありがちなミスで、散布図を描くとなぜ相関係数で判断するのがおかしいのか一発で分かるのだけど、関数入力流れ作業だとなかなか気づかない。僕はかなり初期にここが調べてもなかなか出てこなくて戸惑った経験があった。
次に決定係数あるあるとして、”モデリングしたけどこのモデルの説明具合は?”というビジネス的な課題に対して、AICなりをつかって「相対的なモデル比較しかできない!」ってことに戸惑った経験があったつい最近あった。
ということで相関係数と決定係数の文脈は全然繋がっていないのだけど、上記のような解析ビギナーがぶち当たりそうな課題に対して、検索キーワードの目印の目的で、それぞれ種類についてまとめておく。詳しい計算式などはそれぞれリンクを飛ぶか、Google先生に質問してみてください。
相関係数のいろいろ
・相関係数(ピアソンの積率相関)
量×量の組み合わせに使う。普通に相関係数というとこれ。
・順位相関(ケンドールorスペアマン)
順序データに使う。Rではcor関数のmethod指定で変更できる。心理学でアンケートを扱う時には、5段階などに絞られるので、ポリコリック、テトラコリック相関係数というのも使うらしい。
・相関比
量×質の組み合わせに使う。当たり前だけど相関係数とは0〜1の範囲が同じというだけで、0.7で数字が同じだから・・・といった比較はできない。
・連関係数
質×質の組み合わせに使う。
ココらへんは質と量の検定の種類と合わせて考えてみると理解が深まると思います。
決定係数
・決定係数
正規分布を過程したモデルで最小二乗値から考えるもの。
・疑似決定係数(マクファーデン)
マクファーデンの疑似決定係数が通常使われる。尤度から求められる逸脱度から考えるもので、一般化線形モデルのように、というか正規分布を過程していないものに使う。他にもコックス&スネルなどいろいろある。何が違うかというと、通常の決定係数に ”どう考え方を近づけるか” という視点で “どんな工夫をしているか” が違うというのが個人的な理解。https://stats.idre.ucla.edu/other/mult-pkg/faq/general/faq-what-are-pseudo-r-squareds/
+自由度調整済み・・・
モデルへの当てはまりは説明変数が増えるほど良くなる。そこでペナルティをつけるという考え方。
本当はちゃんとAICなりを使って細かく見ていくのがいいと思うのだけど、ビジネスだと3%しか”説明できてなさそう”なモデルなのか、80%ぐらいは”説明できていそう”なモデルなのかで打ち手への考え方も変わってくると思う。そういう意味で厳格な正確性より実用性が大事だと個人的には思っているて、AICが1下がったからといって気になる変数を除く必要はないし、確率分布の過程が多少強引でも、有益な解釈ができるかどうかのほうが大事だと思う。
結局は予想と実測の間をどういうモノサシで測って、何と比較するかということで最小二乗値からAICまで全部繋がる。なお、上記に書いたのはあくまで代表例で、特定の分野にはそれぞれの指標があることには注意してください。
相変わらずざっくりな記事しか書けませんが笑
ちょうどここらへんモヤモヤしてたんだよね、って人がいれば嬉しいです。
コメントを残す